METODO DE GAUSS

El método de Gauss es una generalización del método de reducción, que utilizamos para eliminar una incógnita en los sistemas de ecuaciones. Se obtiene así un sistema, que llamaremos escalonado, tal que la última ecuación tiene una única incógnita, la penúltima dos incógnitas, la antepenúltima tres incógnitas y la primera todas las incógnitas.

La clave para resolver estos sistemas es seguir el orden para hacer los ceros. Esto se llama escalonar el sistema.

1º Hacemos cero la x de la segunda ecuación reduciendola con la primera ecuación.

2º Hacemos cero la x de la tercera ecuación reduciendola con la primera ecuación.

3º Hacemos cero la y o la z de la tercera ecuación jugando con la segunda y la tercera ecuación.

4º Con el sistema escalonado obtenemos las soluciones.

 

Esto se consigue a partir de la triangulación de la matriz obtenida del sistema de ecuaciones

Por ejemplo, tenemos el siguiente sistema de ecuaciones con tres incógnitas:

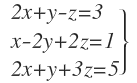
En primer lugar obtenemos su matriz equivalente, que se corresponde a una matriz donde en cada fila colocamos los coeficientes de cada ecuación. Al hacerlo así, los coeficientes de “x” se quedan en la primera columna, los coeficientes de “y” en la segunda columna, los coeficientes de “z” en la tercera columna y los números en la cuarta columna:

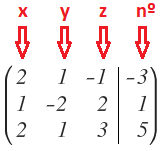
El método de Gauss, como lo he comentado antes, consiste en triangular la matriz del sistema, lo que quiere decir que los elementos que queden por debajo de la diagonal principal tienen que ser igual a cero:

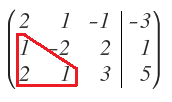
Para triangular la matriz tenemos que ir realizando operaciones elementales entre filas.

Esto puede resultar algo trabajoso, ya que se suelen confundir realizando operaciones y no llegar a obtener el resultado esperado, por ese motivo esta es la metodología que hay que seguir para que la triangulación te salga siempre.

En primer lugar, debemos conseguir que en el primer elemento de la primera fila haya un 1:

En este caso,  tengo un 1 en la fila 2 de al misma columna, luego lo que voy a  hacer es intercambiar la fila 1 por la fila 2:

La matriz nos queda de la siguiente manera:

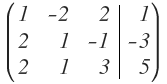
Una vez que tenemos un 1 en el primer elemento de la primera columna, lo siguiente que hay que conseguir es que los elementos que queden por debajo del 1 en la primera columna sean cero:

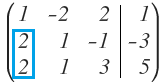
En este caso, para conseguir esto, a la fila 2 le voy a restar dos veces la fila 1 y el resultado lo dejaré en la fila 2:

Y por otro lado, a la fila 3 le voy a restar la fila 2 multiplicada por 2. El resultado de esta operación lo dejo en la fila 3:

La matriz después de operar con las filas 2 y 3 queda de la siguiente manera:

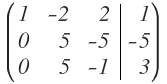
Una vez hemos conseguido tener un 1 y el resto de elementos que sean ceros en la primera columna, tenemos que conseguir que el segundo elemento de la segunda columna sea un 1:

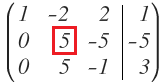
Lo que voy a hacer en este caso es dividir la fila 2 entre 5 y dejar el resultado en la fila 2:

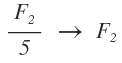Por lo que la matriz queda: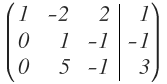

Finalmente, hay que conseguir que el elemento que queda por debajo del 1 en la segunda columna sea un cero:

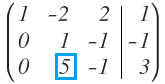
A la fila 3 le resto cinco veces la fila 2 y dejo el resultado en la fila 3:

Quedando la matriz:

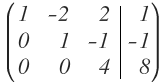
Ya está triangulada la matriz, ya que nos han quedado todo ceros por debajo de la diagonal superior.

Llegados a este punto, volvemos a obtener el sistema de ecuaciones equivalente de esta matriz, teniendo en cuenta que la primer columna corresponde a los coeficientes de “x”, la segunda columna a los coeficientes de “y”, la tercera columna a los coeficientes de “z” y la cuarta a los números.

El sistema de ecuaciones que nos queda es el siguiente:

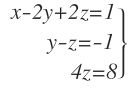
Este sistema ya lo podemos resolver por el sistema de sustitución. Vamos a ir resolviéndolo paso a paso

En la tercera ecuación:

Despejamos z:

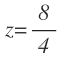
Y operamos para obtener el valor de z:

En la segunda ecuación:

Sustituimos z por su valor:

Despejamos “y”:

Y operamos:

Finalmente, en la primera ecuación:

Sustituimos “y” y z por sus valores:

Operamos:

Despejamos la x:

Y volvemos a operar, obteniendo finalmente el valor de x:

Por tanto, el resultado de este sistema de tres ecuaciones con tres incógnitas es:

Como ves, se trata de ir despejando la incógnita en las ecuaciones donde sólo nos queda una incógnita e ir sustituyendo en el resto de ecuaciones los valores que vamos obteniendo.

El procedimiento para resolver un sistema de cuatro ecuaciones con cuatro incógnitas sería el mismo. Solamente tienes que ir consiguiendo 1 en la diagonal principal y ceros por debajo de ella, columna por columna tal y como hemos ido haciendo en este ejemplo.